Mineral Resource Estimation for Asteroid Mining Projects
Authors: Mark Sonter, Stephen Covey, John S Lewis, & Asha Rao , Deep Space Industries.
This paper reviews and seeks to apply concepts from terrestrial mining exploration, to the tasks of target identification, quantification of contained resource potential, and recovery extraction and return to orbital markets, of mineral values from Near Earth Asteroids.
Introduction:
Discussion in the technical literature of recovery of resources from Near Earth Asteroids has a long history.(e.g.,O’Leary, Kuck, Lewis, Kargel, Sonter,etc.)
The emergence in the last 2 years of two commercial entities intent on recovery of asteroid resources, viz Planetary Resources Inc and Deep Space Industries, prompts a more critical review of the claims, applying to the extent possible, the learnings and concepts of terrestrial resource industries(Elvis).
Concepts:
‘Mineralization’ is material containing values in sufficient concentration that it is technically feasible to consider recovering these values. Mineralization is only definable as ‘Ore’ if it can be economically mined processed and sold to make a profit
A ‘Mineral Resource’ is an occurrence of mineralization that has been shown to have such form ,grade, continuity, quality and quantity as to be economically viable for eventual extraction. Mineral Resources are categorized for reporting to Stock Exchanges as Inferred, Indicated or Measured, depending on the (qualitative) level of geological confidence (generally obtained via direct sampling)in the estimated tonnage and grade
An ‘Orebody’ is a specific volume of mineralization for which a conceptual mine plan and metallurgical processing flowsheet can be developed, which can demonstrably achieve a cost which is low enough to allow an economic operation, and thus make a profit.
An ‘Orebody concept’ is a model describing the geometry, grade, continuity, and mineralogy of an‘ orebody’, in terms (generally) of a hypothesis developed to explain its origin. It is important that the orebody concept is an accurate (or at least realistic) facsimile of reality, because if the concept or model is wrong, then the reserve estimation, mining recovery or both can be wildly in accurate. Note the key role of the Orebody Model both as the basis for the estimation of total ore reserves, and as the basis for developing a mining concept and mine plan.
‘Ore’ is material that we know can be recovered and treated in a specific profitable operation, taking into account operational parameters such as dilution in mining, and metallurgical losses in process, and is classifiable as Proven or Probable Ore (or Mining) Reserves
Discussion:
During the20th Century, concepts of orebody genesis were developed, giving a theoretical background to mineral search campaigns, and there by providing prospective targets for in-field sampling. By the 1970s, there was greatly increased emphasis on formal quantification of mineral resources, for the purpose of prospectus issue and project valuation, and on ore reserves tonnage and grade estimation, for accurate mine and process plant design and costing
In Australia the JORC Code, and in Canada, NI 43-101have been developed (prompted by the Poseidon Nickel selective assay release share-ramping scandal, and the Bre-X sample-salting fraud, respectively), to specify the legal constraints on making public mineral resource and ore reserve statements in pursuit of fund raising efforts for development of mining projects(JORC Code)
In the hard rock mining context(base metals; gold),‘tonnes and grade’ have been(and still are) assessed deterministically, by close-spaced ‘Res Dev’ drilling and sampling of orebodies which are usually irregularly shaped but having well-delineated cut offs, and then interpolating according to various weighting laws to estimate grade in the body of rock between samples(such interpolation being termed ‘kriging’)
In the hard rock mining context(base metals; gold),‘tonnes and grade’ have been(and still are)assessed deterministically, by close-spaced ‘Res Dev’ drilling and sampling of orebodies which are usually irregularly shaped but having well-delineated cut offs,and then inter polating according to various weighting laws to estimate grade in the body of rock between samples(such interpolation being termed ‘kriging’)
Coal, bauxite, and iron ore deposits differ from gold and base metal orebodies, inasmuch as they tend to be extensive, tabular or lenticular, and continuous, with gradational grade and penalty-element content cut offs rather than sharp grade or structural cutoffs. This reduces the need for close-spaced drill out for proof of continuity, and allow sad option of stochastic or probabilistic resource assessment. For such orebodies, the ore-defining parameters are cut off grade, minimum seam thickness(eg, coal), and maximum level of penalty elements(eg phosphorus in iron; silicon in bauxite)
Recent literature has embraced stochastic (probabilistic)methods to alleviate there liance on deterministic (and costly)‘drill pattern’ data, and additionally, to better quantify the risk profile(probability of achievement of) the resource quantification assessments made
Fuzzy mathematics is another way of making explicit the probabilistic nature of resource estimation: this has been pioneered by Bardossy et al in Hungary, and demonstrated in their successful assessment of several small bauxite deposits (Bardossy Szabo & Varga 2003).
‘Resource range analysis’ is a similar technique, which develops, and then multiplies together, probability distributions for each of the various ore-defining and mineral-recovery parameters; and then delivers a probability-distribution of recoverable resource. This approach is used within BHP-Billiton to rank proposed greenfield projects as to investment-worthiness, whilst taking into account the sparseness of early-stage project data (Mullins Carey & Hodson 2003)
The oil & gas industry suffers a similar sparse-data problem in deriving new project resource assessment, in as much as a decision on investment must be made on the basis of a single drill hole, supported by remote sensing (in this case, seismic). They cannot ‘drill out’ a hydrocarbons trap, in the way a minerals exploration team can (and must) when quantifying a base metal orebody
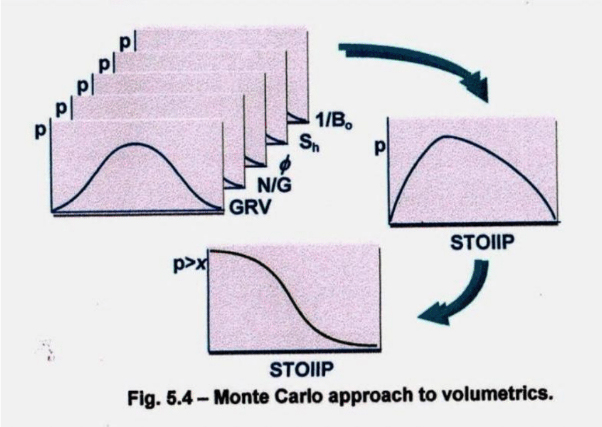
The oil industry thus develops‘ scenario probabilistic’ derived risk-resource estimation distributions, a philosophically-identical but formalistically-different approach to RRA, and uses this to rank wildcat drill hole discoveries, for prioritizing development spend. This is well explained in the Guidelines ofPRMS2011and illustrated in Fig 1.(Chapt 5, Probabilistic Reserves Estimation,WSwinkels)
The philosophical problem arising with discussions of future asteroid mining is that according to the ‘deterministic’ approach to resource estimation, because we cannot realistically undertake wildcat or green fields cout/exploration or in fill drilling, it would appear to be impossible to issue an Inferred, Probable or Measured Resource. “So how will you ever raise money?” How asteroidal resources can come to be quantified in an alternative reasonably robust way, for purposes of project financing and project planning is therefore amost important issue.
The new probabilistic approaches to resource estimation, alluded to above ,improve on the classical deterministic approach, because they can quantify risk of failing to meet various target recoveries, based on general rules and sparse local data. They appear thus to be useful to prospective ‘asteroid miners’ ,in as much as they enable rigor to be applied to ‘risk-based’ statements of resources, even in the absence of site data, using probability distribution based statements of grade, etc
We decided therefore to apply ‘scenario probability analysis’ to synthesize a resource risk probability distribution for the estimation of recoverable resources from certain asteroid types
As background, note that asteroids can be characterized by their reflectivity in visible light, called albedo. Generally speaking, asteroids fall into two broad categories of dark objects(albedo <0.1) and bright (albedo >0.14), with very few in between. Where reflection spectra are available, mineral absorption bands can often be discerned and comparisons can be made with laboratory spectra of known classes of meteorites. A number of these spectral types(C, D, B,F,P, etc.)have very low albedos because of the prevalence of extremely dark materials such as tarry organic polymers(kerogen)and magnetite. The corresponding meteorite samples frequently contain abundant clay minerals and water-soluble salts, contributing to water contents in the bulk rock as high as about22%.The Asteroid Belt, the source of almost all NEAs and meteorites, is about 65% C-type material, which dominates the outer half of the Bel
In the total NEA population, about 30% are dark, but these may contribute the majority of the mass of NEAs less than about 5 km in diameter. The NEA 2008 TC3, discovered by the Catalina Sky Survey on 7 October 2008, was found to be on an impact trajectory with Earth. The reflection spectrum of the incoming asteroid showed a low albedo and a provisional C type identification. Several hours after discovery, this small asteroid (4 m; about 80 tonnes) entered Earth’s atmosphere and exploded. Some800 meteorites have been recovered from this fall, most of which are members of the rare ureilites class of meteorites, very dark and carbon-rich stones with spectra that place them in the F class, closely related to the C class.
In general, the C asteroids and related types will contain from 1% to well over 20% chemically bound water held in clay minerals and in hydrated salts such as gypsum and epsomite. Based on observations of metre-sized fireballs, carbon-rich materials make up the majority of the mass entering Earth’s atmosphere. The D-type asteroids have spectra and orbits typical of short-period comets, which, according to theoretical modelling of their evolution, may contain up to 60% water ice in their interiors, under a fluffy layer of dark carbonaceous dust. The D-type NEA Don Quixote is probably such an ice-rich body
he bright(S and related types) NEAs are dominantly ordinary chondrites, in which the dominant minerals are the iron-magnesium silicate so living and pyroxene, metallic iron-nickel, and the iron sulfide mineral troilite. Their total iron contents range from about 10% to 31% by mass
For potential water orebodies, we restrict our interest to ‘dark’ targets, with albedos below 0.1.
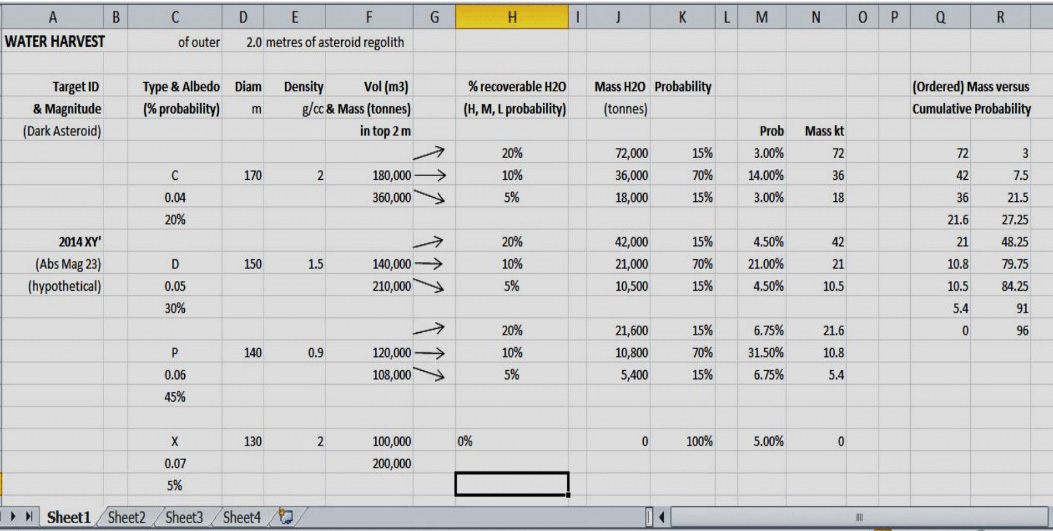
Asteroidal targets with in this restricted albedo range of interest will split probabilistically into several mutually exclusive asteroidal types, the distribution being, we assume, roughly C, 20%; D, 30%; P,45%; and X, 5%. These types have albedos respectively of 0.04, 0.05, 0.06, and 0.07; and bulkdensities of 2, 1.5, 0.9, and 2 t/m3.For each of these types there can be defined a probability distribution which describes the percent likelihood of presence of at least some particular percent-by-mass of (a) water, in water of hydration and as chemically bound in phyllosilicates; and (b) magnetics such as magnetite. Thus, for C types asteroids, we can make a probabilistic statement that the water content by mass in the mineable regolith lies in a range, between 5% at the ‘pessimistic’ end of the scale, and 20% at the ‘optimistic’ end of the scale, as follows
‘There is a 15% probability that the recoverable water content in the mineable regolith of a C-type asteroid will be 5% by mass; there is a 70% probability that the recoverable water in the mineable regolith will be 10% by mass; and there is a 15% probability that the recoverable water will be as high as20% by mass.’
Clearly this is a very ‘granular’ statement, and a more realistic description would be in terms of a continuous probability distribution. However for the purposes of a first-pass worked example it will suffice.
And so on for other types, as indicated in Table 1 below.
For each of several different mutually exclusive ‘orebody models’ we can thus propose a probability distribution for percent likelihood of some minimal percent water recovery in a surface or subsurface mining process.(5)
Table1below shows the totality of the mutually-exclusive scenario probabilities, leading to resource estimates of water extractable from the top 2 metres, for each target-type scenario.(Note that the asteroid can only be C or D or P or X.)
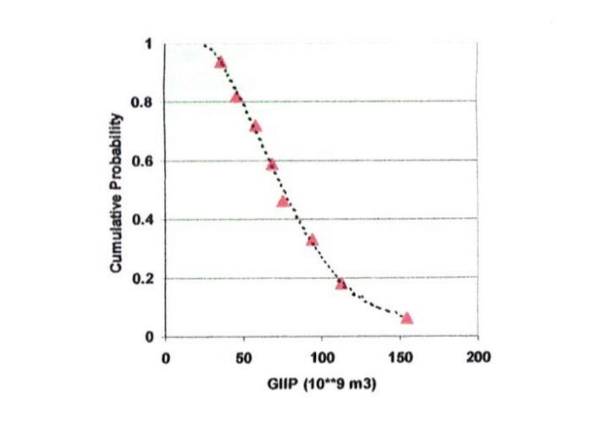
By adding the mutually exclusive scenario probabilities, and by multiplying the mineral presence and recovery probability functions, one can construct probabilistic estimates of mass recovery and hence mining process valuation. The combined cumulative recovery-risk distribution describes the probability of encountering recoverable water no matter which type the target is, and is shown, for water recovery, in Fig2
This outcome is (it should be recognized) a robust (i.e. clearly based) Mineral Resource Estimate, equivalent in concept at least to a JORC or NI 43-101 Inferred Mineral Resource
Note with surprise the high confidence level which the analysis provides!
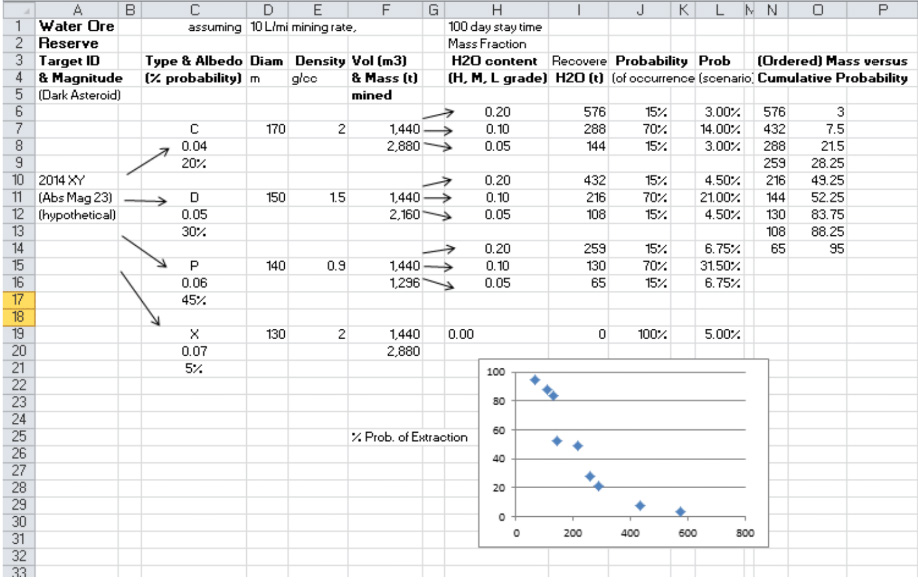
The next stage is to repeat this ‘scenario probability’ exercise, for a specific technical mining method, and overall mission (project) plan. The outcome of this exercise becomes an estimate of Probable Mineable Ore Reserve.
Results are given in Table 2, for the case where the Project Mission assumes a 100 day single season mining period, and mining rate of5kgperminute (and the target description is as before)
The result provides comfort that we can indeed mine and return water from highly accessible near-earth asteroids, and that we can construct a probabilistically-sound prediction of mass return
Conclusion:
It can be seen that these concepts can be successfully applied to provide basis for valuation of asteroid mining missions, and for choosing between competing missions, and thus will become important as would-be asteroid mining companies begin planning commercial missions. As an aside, it is impressive the prospectivity which appears after input of what the authors believe to be realistic but conservative values and distributions, thus bolstering the argument for commercial viability.
Diagrams:

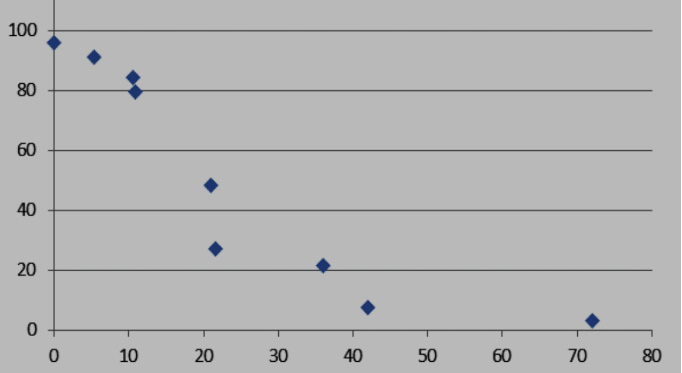
In order to advance from the above probabilistic estimate of mineral resource to an estimate of ore reserve, we need to hypothesize a specific mining plan. Below, as an example, I propose a mining rate of 10 litres per minute, for 100 days as the celestial-mechanics-restricted stay time.
The result is as shownbelow, giving a 50% probability of achieving at least 200 tonnes water recovery, and approximately 80% probability of achieving at least 150 tonnes
Conclusion:
All that is needed then, hypothetically, to make the case close for probable achievement of a target300 tonnes of product, which has been elsewhere identified as an achievable mass return for first generation resource missions,is for the mining rate to be doubled…
So, we need to be able to mine, and cook, 20 litres of regolith per minute, to make this work.
References:
O’Leary B, Mining the Apollo and Amor Asteroids, Science197, 22 July 1977 pp363-366.
Kuck DL, Near-Earth Extraterrestrial Resources, in Space Mfg 3, Proceedings of 4thPrinceton / AIAA Conference, 1979.
Lewis JSet al, eds,The Resources of Near Earth Space, Univ. of Arizona Press, 1993.
Kargel JS, Metalliferous Asteroids as Potential Sources of Precious Metals, J Geophys Research99,25 Oct 1994, pp21129-41
Sonter MJ, The Technical & Economic Feasibility of Mining the Near Earth Asteroids, MSc(Hons)thesis, Univ of Wollongong, 1997.
Elvis M, How Many Ore-Bearing Asteroids? Planetary & Space Science, in press, 2014
The Australasian Code for Reporting of Mineral Resources and Ore Reserves (JORCCode):Joint Ore Reserves Committee, 1999.
Swinkels WJAM, Probabilistic Reserves Estimation: Chapt 5,PetroleumResourceManagementSystem:Guidelines for the Application of the PRMS, Nov 2011. (sponsored by: Soc. of Petroleum Engineers;Amer.Assoc.PetroleumGeologists;WorldPetroleumCouncil;Soc.PetroleumEvaluationEngineers;& Soc. Exploration Geophysicists.)
Bardossy, Szabo, & Varga: a New Method of Resource Estimation for Bauxite and other Solid Mineral Deposits, Jnl of Hungarian Geomathematics, 2003
Mullins MP et al, Mineral Resource Risk Assessment in the BHP-Billiton Capital Investment Process, Appl. of Computers & Operations Research in the Minerals Industries, Sth African Inst. Mining &Metallurgy, 2003.